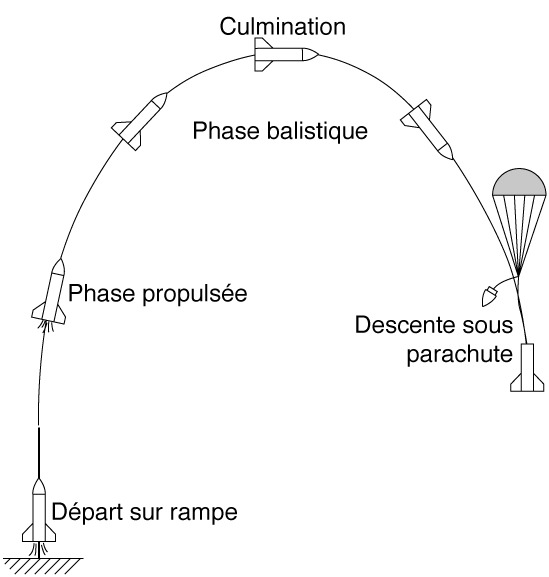
6- LE VOL DE LA FUSÉE
3 ... 2 ... 1 ... ZÉRO
Et la fusée s'élève majuestueusement dans le ciel... Une fusée vole, c'est incontestable, mais comment ? Comme tout véhicule, elle possède un moteur qui la propulse. Mais, pour la micro-fusée, il n'est pas question de chauffeur qui la dirige. Elle doit se guider seule, ou presque, tout au moins sans intervention humaine.
Nous appellerons stabilité cette capacité pour la fusée
de conserver la même attitude (pointée vers le ciel) durant son
déplacement.
Le but de la fusée étant de transporter une expérience
le plus haut possible, ses performances en poids et altitude vont nous
intéresser tout particulièrement. Il va donc falloir lui donner
des caractéristiques telles qu'elle aille vite et loin. Ce sont ces deux
préoccupations que nous aurons dans la conception de la fusée
:
- sa stabilité, qui lui assurera une bonne trajectoire
- ses performances qui la rendront efficace.
LES PHASES DE VOL

LES FORCES EN PRÉSENCE
Trois forces contribuent au déplacement de la fusée :
- la poussée du moteur,
- le poids de la fusée,
- la résistance de l'air à l'avancement de la fusée.
Ces forces peuvent se décomposer suivant les axes longitudinal et latéral de la fusée :
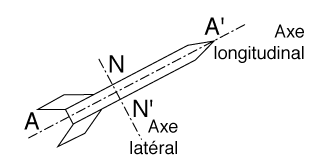
Le poids s'applique au centre de gravité (C.G.) et est dirigé verticalement :
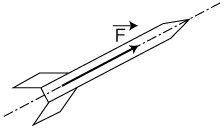
La poussée, si le propulseur est correctement positionné s'applique suivant l'axe longitudinal :
La résistance de l'air à l'avancement de la fusée, qui s'applique en un point appelé «centre de poussée aérodynamique» (C.P.) :
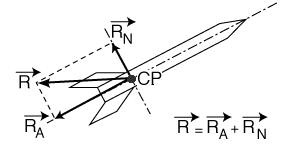
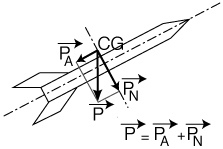
COMPOSITION DES FORCES
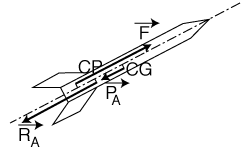
Suivant l'axe longitudinal : les performances.
Les trois forces F, PA et RA sont colinéaires et peuvent s'ajouter :
F + PA + RA = TA
TA, résultante longitudinale des forces sera la force responsable du déplacement longitudinal, donc des performances de la fusée.
Suivant les axes latéraux : la stabilité.
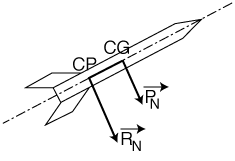
Les deux forces latérales PN et RN normales à la fusée
vont comme pour une balance, faire tourner la fusée autour d'elle-même.
Le mouvement de rotation résultant sera significatif de la stabilité
de la fusée.
SUR QUELLES FORCES AGIR ?
• La poussée du moteur : un seul moyen : changer le type
de moteur, ce qui modifiera les performances, mais n'influera pas sur la stabilité.
• Le poids : défini avant le lancement, il ne varie durant
le vol que de la masse de poudre brûlée et éjectée
pendant la propulsion .
• La résistance de l'air : c'est surtout grâce à
elle que nous aIlons pouvoir améliorer performances et stabilité
de la fusée.
LA RÉSISTANCE DE L'AIR
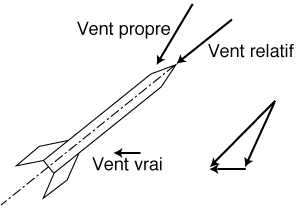
Elle provient de l'action combinée :
- de l'air fixe par rapport à la fusée en déplacement :
le vent propre. La vitesse de ce vent est égale à la vitesse
de déplacement de la fusée.
- de l'air en déplacement pour des raisons météorologiques
: le vent vrai.
Les vitesses de ces deux vents s'additionnent pour ne donner qu'un seul déplacement
d'air apparent : le vent relatif ou apparent.
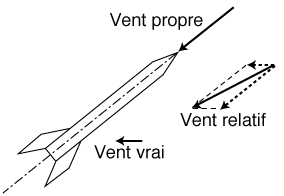
ACTION DU VENT RELATIF
La résistance de l'air est la conséquence de l'existence de ce vent relatif par rapport à la fusée supposée immobile. Elle est de même direction et de même sens que ce vent. Sa valeur (R) est en relation avec le carré de la vitesse (V) de ce vent relatif.
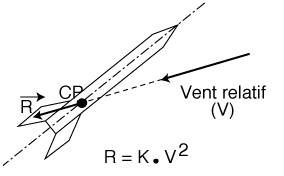
Comme précédemment, nous pouvons décomposer cette résistance en deux composantes.
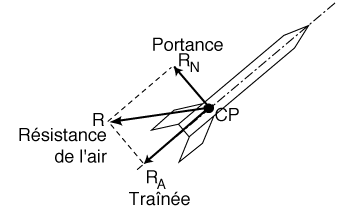
- RA, composante de l'axe longitudinal qui influe sur les performances de
la fusée, est appelée traînée.
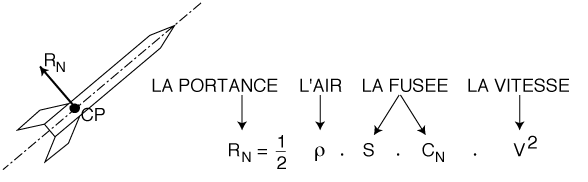
- RN, composante normale à I'axe longitudinal, qui assure la stabilité
de la fusée est appelée portance.
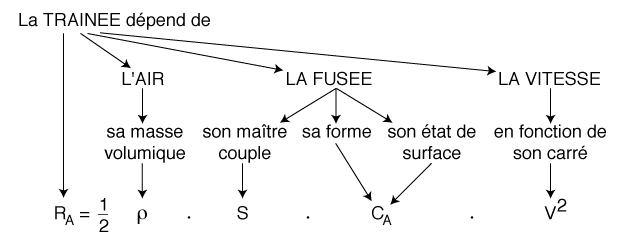
LA TRAÎNÉE
Elle dépend principalement de 3 facteurs :
- la taille de la fusée,
- sa forme,
- son état de surface.
La taille de la fusée, et plus précisément la surface
«vue» par l'air en mouvement : le maître-couple.
Le maître-couple est l'aire de la projection de la fusée sur un
plan perpendiculaire à I'axe du vent relatif.
Dans de bonnes conditions de stabilité, la surface sera prise sur un
plan normal à l'axe longitudinal de la fusée.
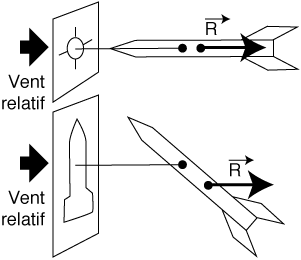
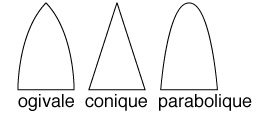
Les formes : les profils de la pointe, des ailerons, et la présence de tout élément extérieur tel un guide de rampe.
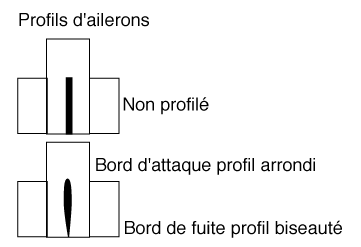
L'état de surface : un revêtement de papier abrasif sera moins performant qu'un vernis poncé finement.
Pour tenir compte pratiquement des deux derniers éléments, la
forme et l'état de surface, le coefficient de traÎnée
CA est introduit .
Le maître-couple S (en mètres carrés) et le coefficient
C (sans dimension), donnent le paramètre S.CA qui représente l'influence
de la construction de la fusée sur la traînée aérodynamique.
Pour être plus rigoureux, nous faisons intervenir l'état de l'air
dans lequel la fusée se déplace, sous la forme de sa masse
volumique. Dans notre cas, cette dernière sera considérée
comme constante.
La portance : L'expression de la portance aérodynamique est identique à celle de la traînée, au coefficient près qui devient coefficient de portance CN et qui prend bien entendu une autre valeur :
COMMENT DIMINUER LA TRAÎNÉE ?
La résistance de l'air (R) est complètement définie
par ses deux composantes :
- La portance (RN) pour la stabilité de la fusée
- La traînée (RA) pour ses performances.
Nous ne présenterons pas ici les valeurs numériques correspondantes
et nous conseillons de se reporter aux notes techniques correspondantes.
Pour la traînée, les solutions telles que réduire le maître
couple, profiler les ailerons et la pointe, améliorer l'état de
surface, apparaissent nettement.
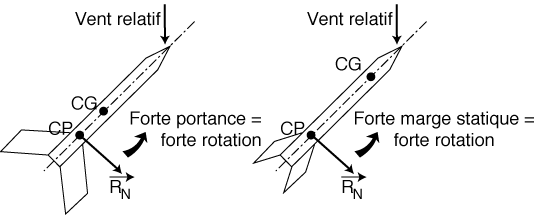
Pour la stabilité, il n'en est pas de même d'autant que la valeur de la portance RN n'est pas seule à intervenir.
LA STABILITÉ DE LA FUSÉE
Pour être stable, la fusée doit conserver la même attitude durant son vol. Pour la micro-fusée, conserver son attitude consistera à maintenir son axe longitudinal aligné avec le vent relatif.
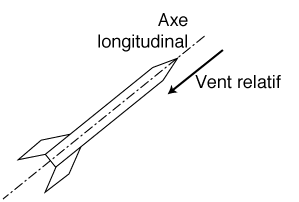
Lorsque cet alignement est rompu, la fusée est dite en incidence. L'angle que fait alors l'axe longitudinal de la fusée avec le vent relatif est l'angle d'incidence.
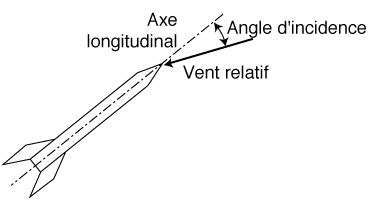
En d'autres termes, si, pour une quelconque cause, la fusée se met en incidence, elle retrouvera sa position initiale (axe longitudinal aligné avec le vent relatif) si elle est stable.
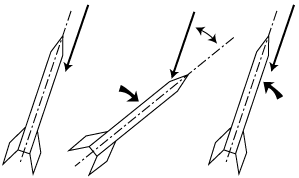
RÉPARTITION DES FORCES NORMALES :
Nous avons vu que les forces qui contribuaient à la stabilité de la fusée sont la composante du poids (PN) et la portance (RN). La portance étant proportionnelle au carré de la vitesse, dès que la fusée a acquis un peu de vitesse (RN) devient prépondérante sur (PN), le rapport d'importance étant d'environ 10.
Ces deux forces normales entraînent la rotation de la fusée.
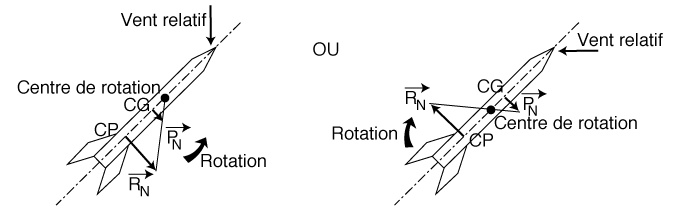
Dans les deux cas, la portance (R ) étant très supérieure à la composante normale du poids (PN), la fusée tourne autour d'un centre de rotation proche du centre de gravité. Elle tourne autour de ce centre dans le sens de la portance. En simplifiant, en négligeant la composante normale du poids, nous pourrons imaginer que la fusée tourne autour du centre de gravité (C.G.) sous la seule action de la portance (RN).
Cette schématisation va nous permettre d'étudier les trois situations
possibles :
- la stabilité,
- I'instabilité,
- I'indifférence.
LA STABILITÉ
Supposons notre micro-fusée se mettant fortuitement en incidence. Si
le centre de poussée (C.P.) est placé en arrière du centre
de gravité par rapport à la pointe, la force de portance entraîne
la fusée qui revient vers sa position initiale. Une fois la fusée
dans cette position, la force de portance s'annule.
En fait, la force de rappel de la portance a tendance à entraîner
la fusée en incidence de l'autre côté du vent relatif, et
c'est seulement après plusieurs oscillations de plus en plus faibles,
amorties, que la fusée retrouve sa position initiale.
L'INSTABILITÉ
Reprenons une micro-fusée dont le centre de poussée soit en avant
du centre de gravité par rapport à la pointe. Dans ce cas, la
force de portance va entraîner la fusée qui va se retourner par
rapport au vent relatif, la pointe en arrière.
Or, le moteur propulse la fusée et le vent relatif est la somme du vent
propre de la fusée (dû à son déplacement) et du vent
vrai. La fusée se retournant, l'axe de propulsion fera de même
et le vent propre également.
Le vent relatif aura donc tendance à suivre l'axe longitudinal de la
fusée.

Comme la position qui convient alors à la fusée est le sens
de la pointe opposé à celui du vent relatif, notre fusée
se comporte comme un serpent qui tente, en vain, de se mordre la queue.
Elle effectuera donc des «loopings» avant de retomber disgracieusement
au sol.
Nous sommes en situation d'instabilité.
L'INDIFFÉRENCE
Reste le cas où le centre de gravité et le centre de poussée
sont confondus. Les deux forces (PN) et (RN) sont alignées et la fusée
n'est pas soumise à rotation. Elle va errer en une quelconque position.
En fait, en cours de vol, centres de gravité et de poussée ne
sont pas fixes (déplacement du centre de gravité par éjection
des gaz du moteur, déplacement du centre de poussée en fonction
de l'attitude de la fusée...) .
L'indifférence consiste donc plus en une alternative entre stabilité
et instabilité, difficilement évaluable avant le vol.
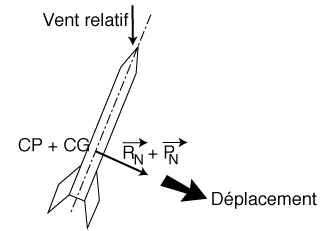
DÉTERMINATION DES CENTRES
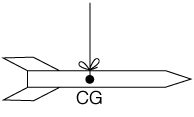
• LE CENTRE DE GRAVITÉ
Par définition, il est situé sur l'axe longitudinal au niveau de la position d'équilibre au repos de la fusée à I'horizontale.
• LE CENTRE DE POUSSEÉ
Une seule solution reste à retenir pour avoir une fusée stable
: le centre de poussée est en arrière du centre de gravité
par rapport à la pointe. Or, pour une micro-fusée simple,
le facteur essentiel pour la position du centre de poussée est la position
des ailerons.
En effet, lorsque la fusée est en incidence, la résistance de
l'air la plus grande sera portée sur les parties de plus grande surface
au vent. Lorsque nous voyons une fusée de profil, il apparaît bien
que la résistance de l'air minimale s'applique sur la pointe et la résistance
maximale vers les ailerons.

La fusée ressemble alors à une girouette dont l'axe de rotation serait placé au centre de gravité, au détail près que la girouette ne possède pas de vent propre donc que son vent relatif est le seul vent vrai.
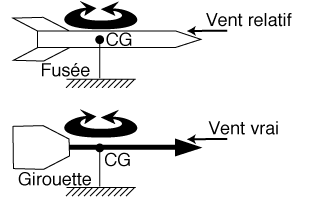
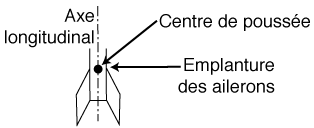
La position du centre de poussée est donc en relation avec la position des ailerons.
C'est ainsi qu'en faisant une grossière approximation sur les ailerons de proportions moyennes, le centre de poussée se situe sur l'axe longitudinal de la fusée, à la hauteur de l'emplanture des ailerons.
TROP DE STABILITÉ NUIT
Il apparaît en résumé que deux facteurs principaux
interviennent dans la stabilité :
- la valeur de la portance qui est en relation directe avec la surface
et la forme des ailerons.
- les positions relatives du centre de gravité et du centre
de poussée.
La distance entre le centre de gravité et le centre de poussée se nomme marge statique.
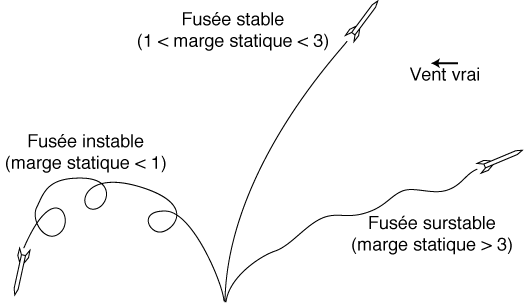
Ces deux facteurs, la portance et la marge statique, sont inclus dans des fourchettes. En effet, supposons tout d'abord que la portance ou la marge statique soient trop faibles. La rotation de rappel sera elle-même faible, à la limite de l'indifférence.
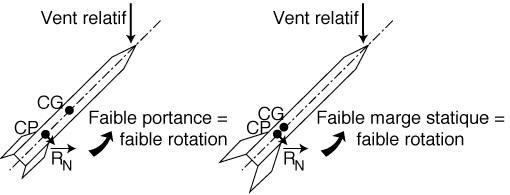
Dans le cas contraire, si la portance ou la marge statique sont très fortes, la force de rappel sera très vigoureuse, renverra la fusée de l'autre coté du vent relatif et la fusée oscillera continuellement sans jamais trouver de position d'équilibre. Cette attitude est nommée surstabilité.
Un autre inconvénient de cette surstabilité a rapport avec le vent vrai (vent météo). Ainsi, lorsque la fusée est stable, elle aligne son axe longitudinal avec le vent relatif, donc en partie avec le vent vrai. Ceci signifie que la fusée a tendance à remonter le vent.
De plus, cette situation n'est pas statique : le vent propre cherche à s'aligner sur le vent relatif, qui lui-même se rapproche du vent vrai et la fusée se couche lentement dans le vent vrai.
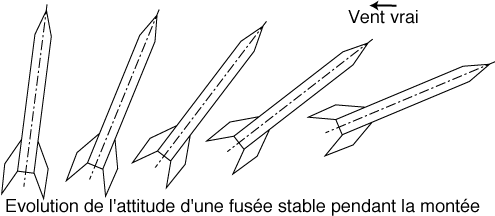
Dans le cas d'une fusée surstable, la fusée se couchera presque immédiatement dans le vent vrai et partira quasiment horizontalement, ce qui n'est pas le but recherché.
CONDITIONS DE STABILITÉ
De manière expérimentale, il est possible d'arrêter
des conditions moyennes de stabilité :
- la marge statique doit être comprise entre 1 et 3 calibres (le calibre
vaut un diamètre de fusée).
- chaque aileron (parallélogramme) doit avoir une envergure comprise
entre 1 et 2 calibres, une hauteur comprise entre 1 et 3 calibres, le nombre
minimal d'ailerons étant de trois.
Attention, ces valeurs ne sont nullement limitatives car les fusées peuvent voler et très bien voler hors de ces limites. Mais, ces valeurs donnent un ordre de grandeur de ce qui est couramment utilisé.
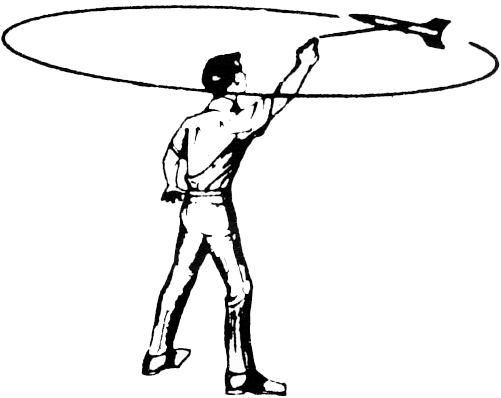
L'ESSAI FINAL
Avant le vol réel, il est préférable de faire un essai
de notre fusée. Pour ce faire, il est possible soit d'utiliser une soufflerie
en suspendant la fusée en son centre de gravité ; soit, plus simplement,
de faire tourner la fusée au bout d'une ficelle fixée en son centre
de gravité.
Si la fusée est stable aux basses vitesses de l'essai, elle le sera bien
entendu aux grandes vitesses du vol.
LES PHASES DU VOL
En guise de conclusion, nous vous invitons à faire voler votre fusée !
Plusieurs séquences se dérouleront dont chacune possède ses propriétés : le départ sur rampe, la propulsion, le vol balistique, la descente sous parachute (si tout se passe bien). Les nombreuses forces augmentent et diminuent au gré de l'évolution de la fusée, et il y aurait encore beaucoup à dire sur ce sujet.
Car la mécanique du vol est une longue histoire...